1 Interval Scheduling

Course Overview¶

• Modules Covered:
  1. Divide and Conquer (FFT, Randomized algorithms)
  2. Optimization (greedy, dynamic programming)
  3. Network Flow
  4. Intractibility and coping strategies
  5. Linear Programming
  6. Sublinear and Approximation Algorithms
  7. Advanced Topics

---

Key Complexity Classes¶

• P: Solvable in polynomial time (e.g., shortest paths in \(O(V^2)\)).
• NP: Verifiable in polynomial time (e.g., Hamiltonian Cycle detection is NP-complete, but verification is easy).
• NP-Complete: A problem in NP that is as hard as any problem in NP. Solving one in polynomial time would solve all NP problems.

---

Interval Scheduling¶

Problem: Select a maximum subset of non-overlapping requests.
Each request has:
- Start time \(s(i)\)
- Finish time \(f(i)\) (with \(s(i) < f(i)\))

Compatibility: Two requests \(i\) and \(j\) are compatible if:
\(\(f(i) \leq s(j) \quad \text{or} \quad f(j) \leq s(i)\)\)

Example:

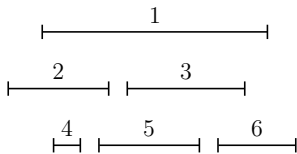
Requests 2 & 3 are compatible; 4, 5, 6 are compatible; 2 & 4 are not.

---

Greedy Algorithms for Interval Scheduling¶

Claim: Greedy algorithm with earliest finish time yields an optimal solution.

Possible Greedy Rules:¶

1. Earliest Start Time
   
   Fails for overlapping long intervals.

2. Smallest Interval
   
   Fails if small intervals block larger compatible ones.

3. Fewest Conflicts
   
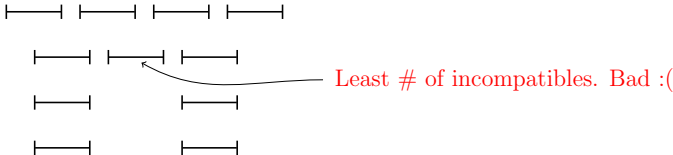
   Computationally expensive to track conflicts.

4. Earliest Finish Time
   Optimal.

---

Proof of Optimality for Earliest Finish Time¶

Inductive Proof:
- Base Case: \(k^* = 1\) – trivial.
- Inductive Step: Assume optimality holds for \(k^*\). For \(k^* + 1\):
- Let \(S^*\) be the optimal schedule. Greedy picks \(i_1\) with \(f(i_1) \leq f(j_1)\).
- Construct \(S^{**} = \{i_1, j_2, \ldots, j_{k^*+1}\}\), which is also optimal.
- Residual problem \(L'\) (intervals after \(f(i_1)\)) has optimal size \(k^*\). By induction, greedy on \(L'\) gives \(k^*\) intervals.
- Total schedule size: \(1 + k^* = k^* + 1\).

---

Weighted Interval Scheduling¶

Problem: Maximize total weight of non-overlapping requests.
- Greedy fails due to weights.
- Dynamic Programming Approach:
Define \(R^x = \{j \mid s(j) \geq x\}\). Recurrence:
\(\(\text{opt}(R) = \max_{1 \leq i \leq n} \left( w(i) + \text{opt}(R^{f(i)}) \right)\)\)
- Time: \(O(n^2)\) (can be optimized to \(O(n \log n)\)).

---

Non-Identical Machines¶

Problem: Schedule jobs on \(m\) machines where each job \(i\) can only run on a subset \(Q(i) \subseteq \{T_1, \ldots, T_m\}\).
- Complexity:
- Decision version ("Can \(k \leq n\) jobs be scheduled?") is NP-Complete.
- Optimization version ("Maximize scheduled jobs") is NP-Hard.

---

Coping with Intractability¶

1. Approximation Algorithms: Guarantee near-optimal solutions in polynomial time.
2. Pruning Heuristics: Reduce search space for practical instances.
3. Greedy Heuristics: No guarantees but perform well empirically.

---