Lecture 2: Divide and Conquer¶

Paradigm¶

• Given: A problem of size \(n\).
• Divide it into subproblems of size \(\frac{n}{b}\), where \(a \geq 1\), \(b > 1\).
• Solve each subproblem recursively.
• Combine solutions to form the overall solution.

Recurrence Relation:
$$
T(n) = a T\left(\frac{n}{b}\right) + [\text{work for merge}]
$$

---

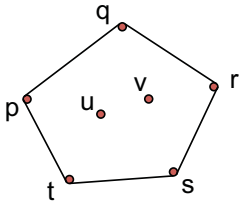
Convex Hull¶

Problem Definition¶

• Input: \(n\) points in the plane:
  $$
  S = \left{ (x_i, y_i) \mid i = 1, 2, \ldots, n \right}
  $$
• Assumptions: No two points share the same \(x\)- or \(y\)-coordinate; no three points are colinear.
• Output: Convex Hull \(\text{CH}(S)\), the smallest polygon containing all points in \(S\).

Brute Force Approach¶

• Test each line segment to determine if it is an edge of the convex hull:
• If all other points lie on one side of the segment, the segment is part of the convex hull.
• Complexity: \(O(n^3)\) (testing \(O(n^2)\) edges with \(O(n)\) checks per edge).

---

Divide and Conquer Approach¶

1. Sort points by \(x\)-coordinate (\(O(n \log n)\)).
2. Divide \(S\) into left half \(A\) and right half \(B\).
3. Recursively compute \(\text{CH}(A)\) and \(\text{CH}(B)\).
4. Merge the two convex hulls.

Merge Step¶

1. Find Upper Tangent \((a_i, b_j)\) and Lower Tangent \((a_k, b_m)\).
2. Link \(a_i \rightarrow b_j\), traverse down \(B\) to \(b_m\), link \(b_m \rightarrow a_k\), and return to \(a_i\).

Example:

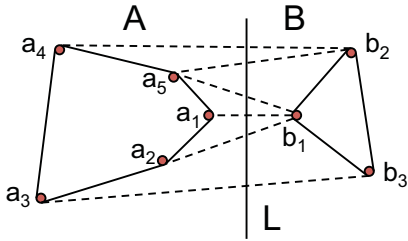
- Upper Tangent: \((a_4, b_2)\).
- Lower Tangent: \((a_3, b_3)\).
- Merged Hull: \((a_4, b_2, b_3, a_3)\).

Finding Tangents¶

• Upper Tangent: Maximizes \(y(i, j)\), where \(y(i, j)\) is the \(y\)-coordinate of the intersection between the vertical separating line \(L\) and segment \((a_i, b_j)\).
• Algorithm:
  1. Initialize \(i = 1\), \(j = 1\).
  2. While \(y(i, j+1) > y(i, j)\) or \(y(i-1, j) > y(i, j)\):
  • If \(y(i, j+1) > y(i, j)\): \(j = j + 1 \mod q\).
  • Else: \(i = i - 1 \mod p\).
    3. Return \((a_i, b_j)\).
• Time Complexity:
  $$
  T(n) = 2 T\left(\frac{n}{2}\right) + \Theta(n) = \Theta(n \log n)
  $$

---

Median Finding¶

Problem Definition¶

• Rank of \(x\): Number of elements \(\leq x\).
• Goal: Find element with rank \(\left\lfloor\frac{n+1}{2}\right\rfloor\) (lower median) or \(\left\lceil\frac{n+1}{2}\right\rceil\) (upper median).

Algorithm: SELECT¶

1. Pick \(x \in S\) cleverly (median of medians).
2. Partition \(S\) into \(B = \{y \in S \mid y < x\}\) and \(C = \{y \in S \mid y > x\}\).
3. Recurse on \(B\) or \(C\) based on \(k = \text{rank}(x)\):
   - If \(k = i\), return \(x\).
   - If \(k > i\), return \(\text{SELECT}(B, i)\).
   - If \(k < i\), return \(\text{SELECT}(C, i - k)\).

Median of Medians¶

1. Arrange \(S\) into columns of size 5.
2. Sort each column (linear time).
3. Recursively compute the median of medians.

Recurrence:
$$
T(n) =
\begin{cases}
O(1), & \text{for } n \leq 140, \
T\left(\left\lceil\frac{n}{5}\right\rceil\right) + T\left(\frac{7n}{10} + 6\right) + \Theta(n), & \text{for } n > 140.
\end{cases}
$$

Proof Sketch:
$$
T(n) \leq cn \quad \text{(by induction, using } \frac{n}{5} + \frac{7n}{10} < n\text{)}.
$$

---

Appendix¶

Example: Tangent Identification¶

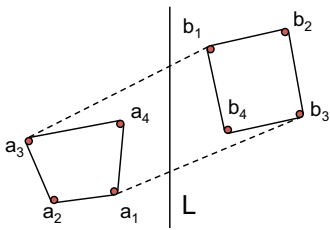
- Upper Tangent: \(a_3, b_1\).
- Lower Tangent: \(a_1, b_3\).
- Note: Tangents need not involve the highest/lowest points.